Demo: Epimorphism

Gene Shuman

Epimorphism is an art project which simulates video feedback in a mathematically interesting, fractaline, and aesthetically pleasing fashion. It is written in the language PureScript, a dialect of Haskell which compiles to Javascript, and runs in users' web browsers.

Overview

How it works

Epimorphism is a digital simulation of video feedback. Video feedback is a traditionally analog art form which has existed in the form of kaleidoscopes & other mirror based systems throughout history and then since the 1960s using video technology to create recursive & self similar animated systems. The basic modern concept is simple, and requires only a video input source(camera) and an output source(screen). The output of the camera is routed to the screen and the camera is then pointed at this information, using the output of the camera(with some time delay) as its input. In the simplest example, where the camera is slightly zoomed out, you see an image of the screen as it was a few(n) ms previously. In the inner screen you see an image of the screen as it was 2*n ms ago, and so forth. The situation can get significantly more interesting when you rotate the camera, adjust the zoom, add filters, add external imagery, etc, and quite often the system can become chaotic, which is a common characteristic of recursive systems.


A traditional video feedback system can be mathematically modeled by a transfer function T where

f(t') = T(f(t))

f(t) = the video frame at time t
T = the transfer function of the camera + display combination


We can expand this further as:

f(t', x) = T(f(t), x) = C(f(t, S(x)) + Ext(t, x))

x = the 2d coordinate we are intrested in finding the color value of
C = the color transfer function of the system, usually an artifact of imperfect color reproduction/display
S = the spatial transfer function of the system, such as camera zoom, pan or rotation.
Ext = external information entering the system - the edges of the screen, hands waving, etc

The Epimorphism software project attempts to expand upon these ideas by digitally simulating this process, adding fidelity, precision and breadth of possibility to the system. A virtual framebuffer is maintained and the above equation applied. We can immediately see many ways in which the analog situation can be improved upon & expanded. For the color transfer function, we no longer have to deal with imperfect color reproduction and loss of saturation inherent in cameras & displays. We are free to use this part of the pipeline in an explicitly asthetic capacity as well. We are also no longer constrained to the basic affine transformations supported by a camera such as zoom, pan & rotation. Epimorphism makes extensive use of elementary complex transformations such as those used in computing the Mandelbrot & Julia sets, lending the system a distinctly fractaline appearance. We are also no longer constrained to manually inserting external information into the system. We can now seed the system with arbitrary shapes & textures.

Technology

The current iteration of the project is written largely in PureScript, a dialect of Haskell. The project is open source and can be found here. The PureScript component of Epimorphism acts as the front end for a parallel/high performance computing application which runs directly on the clients graphics hardware via pixel shaders & WebGL. The frontend of the application is responsible for the WebGL interface, application UI, pixel shader compilation, state evolution, and maintaining and modulating the pattern library. The backend of the application is responsible for implementing the feedback transfer function above. It is a highly parallel application, where the color value of each pixel is computed in its own thread directly on the graphics hardware. The backend of the application is a highly parameterized system, taking each of the above sub-transfer functions and breaking them down further, creating a very high dimensional parameter space for the system. The default mode of operation of the system is a random walk through the parameter space; numerical parameters, as well as transfer functions themselves are animated and interpolated by the front end of the software. Interactive modes of the software are also available, exposing the parameter space to the user. Previous versions of the software have enabled MIDI, OSC, TCP, and basic audio information to control the system as well, however these features have not been ported to the current version of the application.

Live Demo

A beta version of the software is currently live. An interactive demo is proposed to be given at FARM 2016 which intends to covers the topics mentioned herein and provide a more detailed exploration of the parameter space of the system.

PureScript & Functional Programming

PureScript is a relatively new functional programming language inspired by Haskell which compiles directly to javascript. PureScript borrows heavily from Haskell - it shares a very similar syntax, is strongly statically typed, supports type inference, has immutable data, ADT's, pattern matching, type classes, and so on, with the major high level difference being that in PureScript evaluation is strict. There is a collection of more trivial differences, but the language should be easily picked up by anyone fluent in Haskell.

Why Functional Programming
The problem domain at hand here admittedly doesn't lend itself to any particularly elegant representation as compositions or in terms any of other major functional paradigms, so you may ask why use a functional programming language for this project at all, given that we're regularly doing such non-functional things as interfacing with state machines(WebGL) and mutating various data structures(which represent the video output of the system) when it seems that there is little to no domain specific justification? The answer is simply that the inherent benifits of writing purely functional programs(even when not in a particularly functional problem space) are more than sufficient to justify the use of functional programming. Development on this project has been faster, more stable, less error prone, and the software has been easier to reason about and to return to after significant developmental pauses. These are the commonly touted benefits of functional programming, and they have been realized here, allowing for greater a focus to be brought upon the artistic qualities of the software.

A fact of particular note here is that the parameter space of the system is immense and is exceedingly difficult to navigate successfully. The major motiviation for persuing a functional approach to this software was to acheive very fundamental level of stability of the core software/system, freeing up conceptual resources to devote to the core problem at hand - an exploration of the capabilities of the system.

Why Purescript

The project is intended to target as wide of an audience as possible, as easily as possible - in particular anybody with a web-browser which supports WebGL 1.0. The software has been tested on all major web browsers as well as several other platforms, and this breadth of support is possible because of the ubiquity of support for HTML5 applications. PureScript is one of the more powerful, well developed, and easy to use entries in the fairly small space of functional + web. Furthermore, its similarities to Haskell, a language with an immense body of associated technical sophistication and breadth directly increase the power of the language. A large array of sophisticated technologies from the Haskell ecosystem are either directly or easily accessible.

History/Future

The software has been in development in some form for ~10 years, and is currently in its 3rd major rewrite, with the majority of significant features from the previous applications largely functional. Significant near term plans for the software include audio responsiveness, a more detailed & user accessible creation UI, and implementing machine learning algorithms to more adeptly navigate the phase space of the software, possibly even tailoring the results to users individual tastes. An algorithm to ray trace a generalized version of the software in 3 dimensions using distance fields has also been developed but technology is currently lacking. However back of the envelope calculations suggest that consumer hardware is only about 2 generations away from being able to support this idea :)

Details

Parameter Space

We can textualize the expanded transfer function above:

f(t', x) = T(f(t), x) = C(f(t, S(x)) + Ext(t, x))

as follows:
This process naturally divides the parameter space into 3 major subspaces corresponding to the functions C, S, & Ext respectively. There is an additional subspace, a post-processing layer, which is not a part of the feedback system and is currently used to palletize the resulting image.

S(x)

The first thing we do in this subspace is to consider the paramater x as the complex variable z. Complex functions provide us with a wide array of simple & aesthetic 2d planar transformations. All of the basic camera operations can be simply realized by the family of linear functions S(z) = a * z + b.

Currently the system implements all of the 1-1 elementary complex functions (sin,cos,exp,sinh, etc) along with all of the basic compositions(addition, multiplication, composition, etc) avaliable, resulting in a very large space of possible spatial transformations. The transformation functions are often parameterized, i.e S(z) = a * exp(z + b), and these constants a, b are animated by the front end of the system, often moving on linear or polar curves.

A very noticable effect at play here is a result of the fact that our framebuffer is of finite size. In particular, what is stored in memory as the previous frame is considered to represent the square from -1-i -> 1+i in the complex plane. The function S(z) does not always return a value in this region, so we reduce the value to this square via the use of a standard mirrored repeat, which is basically a modular opperation to the given square, but one which preserves continuity. This 'feature' is directly responsible for the kaleidoscopic quality of the system.

Ext(t, z)

The Ext function, in the case of a camera based system, provides external information into the feedback loop. In a virtualized system, such an analogy is slightly askew, and it is preferred to think of this function as Seed(t, z), which seeds the feedback system with information. This subspace is the largest in some sense, and the most unexplored, as literally any 2 dimensional image can be used as a seed. Currently implemented is a parameterized system, composed of 3 layers. Each layer provides some basic geometric shape(lines, boxes, circles), which is then textured, either procedurally(via a gradient, etc), or via an uploaded png image from the texture library. The texture library currently includes a variety of images, from geometric patterns, psychedelic paintings, vectorized drawings, floral and ornate embelishments, and pictures of cats :)

C

There are several color transformation functions currently implemented. The simplest of these are the various color channel (rgb) permutaions. A step above this in complexity are simple modifications in hsv space, often just a hue rotation. For instance, on each cycle of the animation the hue of the previous itterations could be rotated n degress. Also implemented is a modification of the hsls double cone where the space is compressed into a sphere, an arbitrary axis is chosen, and a rotation is performed.

A high level abstraction away from colorspaces is currently in progress, in which the values stored in the feedback framebuffer are not directly interpreted as points in a color space, but more generally as points on an arbitrary 3 dimensional manifold. The color transformation C can then be thought of as an arbitrary morphism of the manifold to itself. The color value of the resulting frame can then be produced via the post processing layer as an arbitrary mapping of the manifold to an existing colorspace (rgb, hsv, etc). This abstraction frees us from having to think about such thorny concepts as composing coloring transformations, which can be difficult to reason about unless the transformation is something like a rotation.

Detailed Example

To provide more insight into the workings of the system, we provide a more in depth explanation of how to create the image on the left, and the specific functions used to do so.

In analogy to traditional camera/tv based feedback systems, we begin with something resembing the edges of a tv screen.
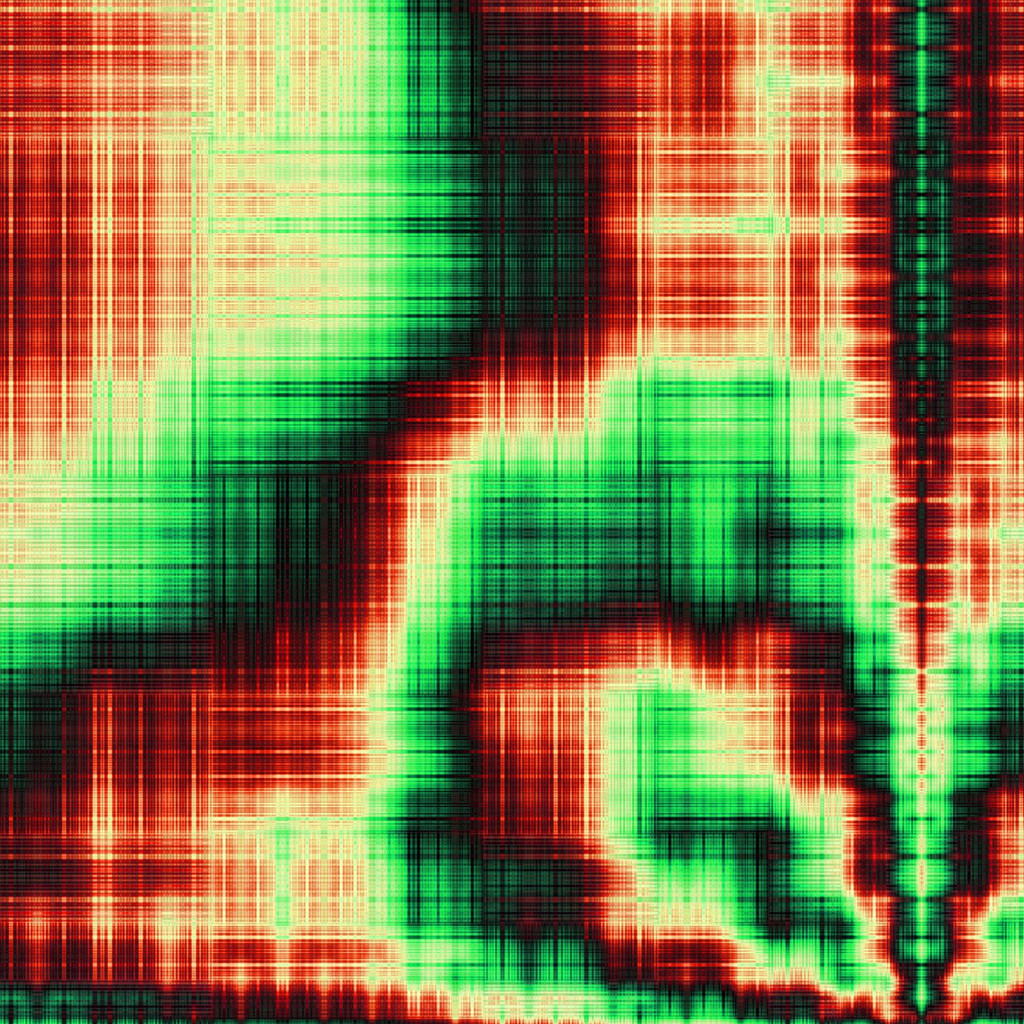
  • S(z) = z
  • Seed = a red frame, textured by a gradient
  • C = id

We 'zoom out' slightly.
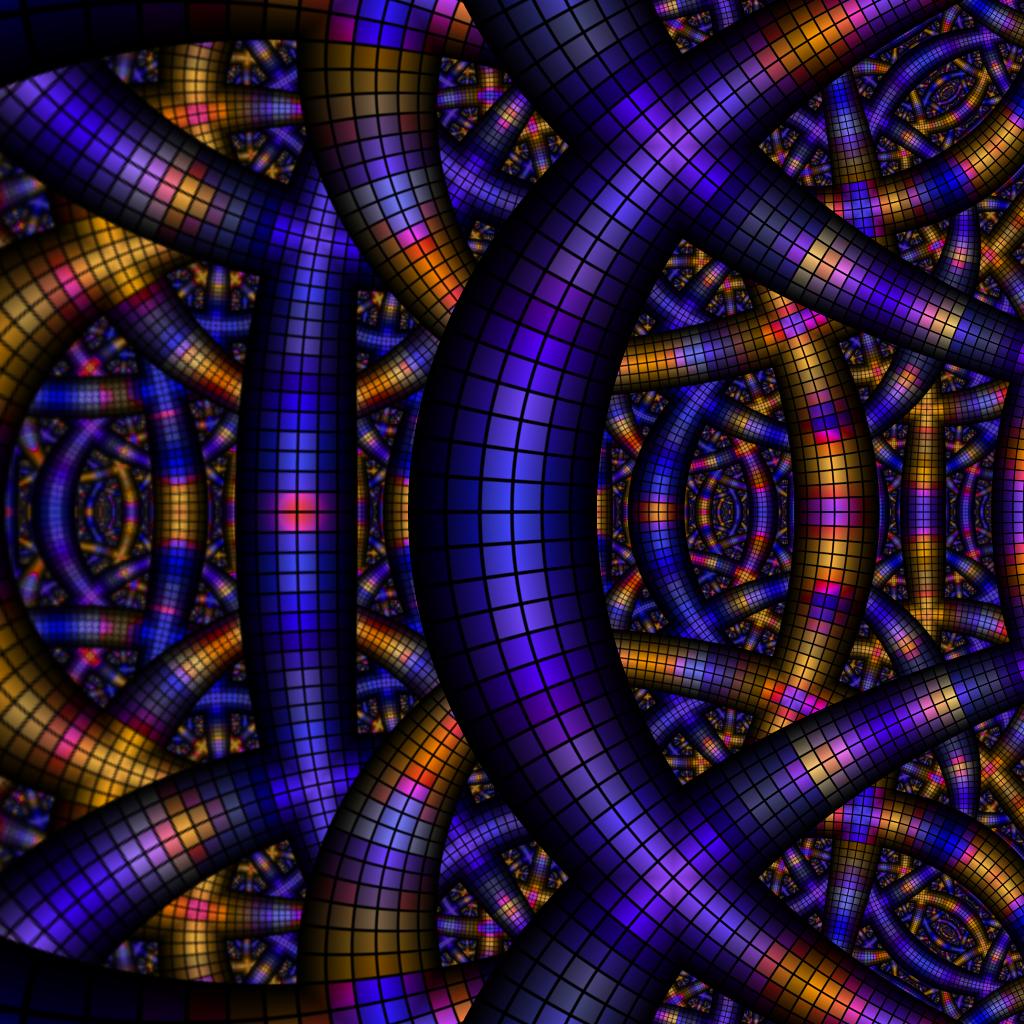
  • S(z) = a * z, a = 1.1
  • Seed = a red frame, textured by a gradient
  • C = id

Upon each itteration, we rotate the hue of the previous frame by 4°
  • S(z) = a * z, a = 1.1
  • Seed = a red frame, textured by a gradient
  • C = rotate hue by α, α = 4°

Begin using a more interesting spatial transformation. Some of the self symmetry here is due to the feedback nature of the system, however the symmetry introduced by the mirrored repeat is also clearly visible.
  • S(z) = a * e z, a = 1.1
  • Seed = a red frame, textured by a gradient
  • C = rotate hue by α, α = 4°

Replace the gradient in the frame by a texture.
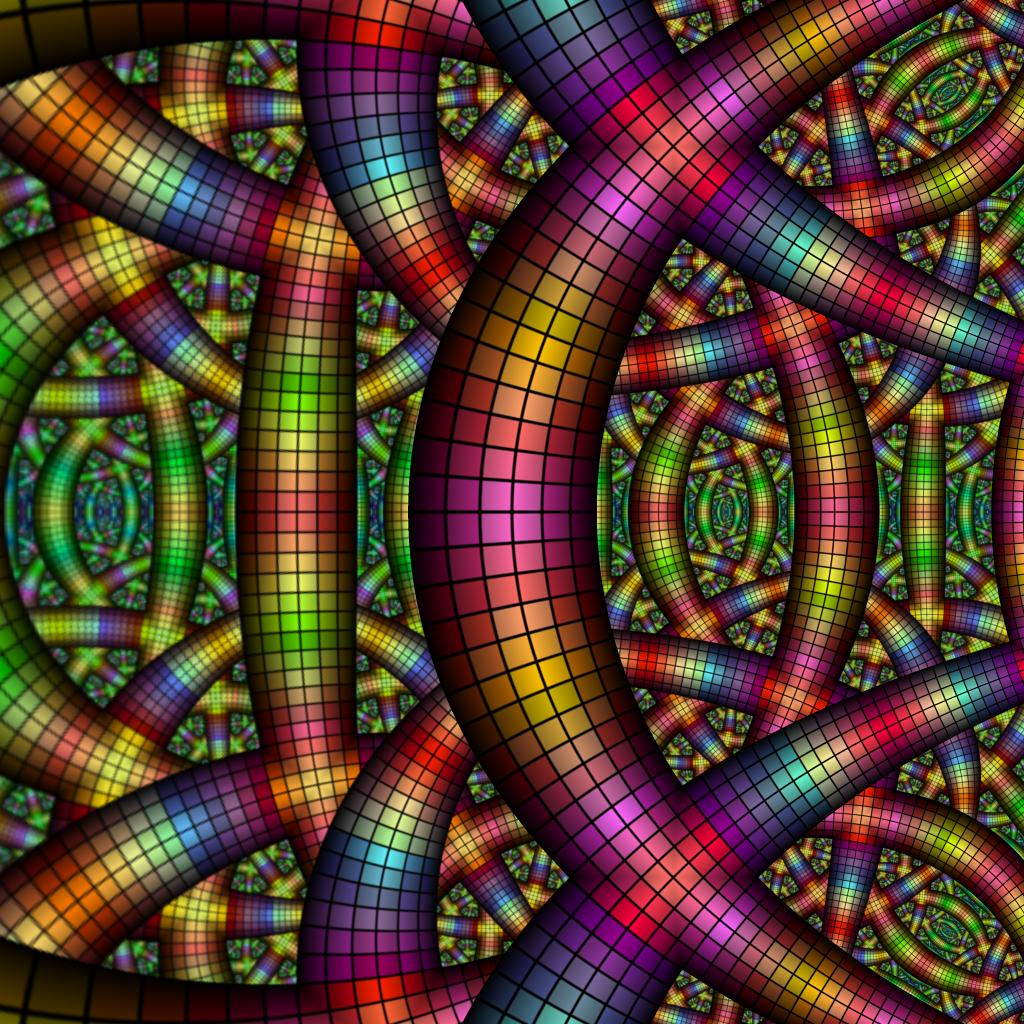
  • S(z) = a * e z, a = 1.1
  • Seed = a frame, textured by the above image
  • C = rotate hue by α, α = 4°

Increase the rotation of the hue.
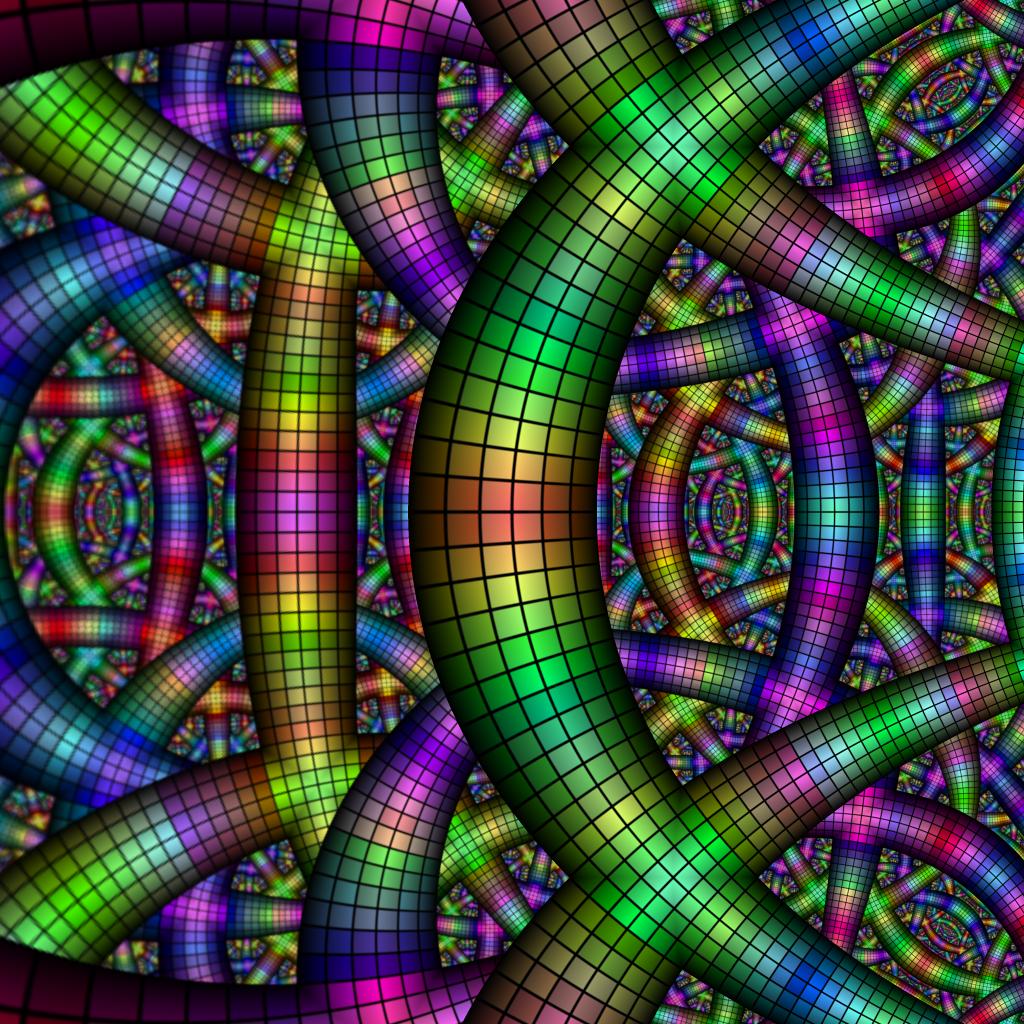
  • S(z) = a * e z, a = 1.1
  • Seed = a frame, textured by the above image
  • C = rotate hue by α, α = 15°

Add a post processing effect to palletize the image
  • S(z) = a * e z, a = 1.1
  • Seed = a frame, textured by the above image
  • C = rotate hue by α, α = 15°
  • Post = limit the colors to blues & oranges

Gallery

The images included in this document have been aggregated over the years from various versions of the application, however they are all currently within the scope of the current application version. Unfortunately, though, the details of the particular parameterizations of the images have been lost to the ages. With the exception of the last three images below, the following were produced entirely procedurally, with no external texturing.